Algoritmos genéticos
Los algoritmos genéticos son una meta-heurística inspirada en la selección natural para solucionar problemas de búsqueda, combinatoria o optimización.
A partir de un conjunto de posibles soluciones a un problema, el algoritmo selecciona las mejores soluciones y las combina, para así, ir mejorando continuamente las soluciones de ese conjunto, hasta encontrar una que tenga las características que buscamos.
Algoritmo
A lo largo del algoritmo se mantiene un conjunto de posibles soluciones al problema, denominado población. Esas soluciones, que también son llamadas individuos, se califican con una función de aptitud, para así saber si una solución es mejor que otra. Los algoritmos genéticos son iterativos y a la población correspondiente a una iteración se le llama generación.
Los algoritmos genéticos necesitan de algunos operadores para poder funcionar:
- Operador de mutación: modificar una solución.
- Operador de recombinación: combinar dos soluciones para producir dos nuevas.
- Inicialización de la población: producir el conjunto inicial de posibles soluciones al problema, sobre el que va a trabajar el algoritmo.
- Operador de selección: función no-determinística para seleccionar soluciones de acuerdo a que tan aptas son.
Además para iniciar necesitamos definir los siguientes parámetros:
- \(n\): Tamaño del conjunto de soluciones (tamaño de la población).
- \(f(x)\): Una función de aptitud.
- Un objetivo: minimizar o maximizar.
- Un criterio de fin de búsqueda.
- Probabilidad de mutación \(p_m\)
- Probabilidad de recombinación \(p_r\)
Cada uno de esos elementos serán discutidos en las siguientes secciones con más detalle.
El algoritmo funciona de la siguiente manera:
- Inicialización:
1.1. Se crea una población inicial \(\mathbb{P}:\{ x_1 ... x_n\}\)
1.2. Se evalúa la calidad de cada solución \(x_i \in \mathbb{P}\) con la función de aptitud. - Búsqueda:
2.1. Se seleccionan 2 individuos de nuestra población (\(x_i,x_j \in \mathbb{P}\))
2.2. Se aplica el operador de recombinación a los dos individuos con probabilidad \(p_r\), generando (\(\hat{x_i},\hat{x_j}\))
2.3. Se aplica el operador de mutación sobre \(\hat{x_i}\) y \(\hat{x_j}\) con probabilidad \(p_m\)
2.4. Evaluar aptitud \(f(\hat{x_i})\) y \(f(\hat{x_j})\)
2.5. Agregar \(\hat{x_i}\) y \(\hat{x_j}\) a conjunto de soluciones nuevas \(\hat{\mathbb{P}}\)
2.6. Repetir pasos desde 2.1 hasta 2.6 hasta que \(\mid \hat{\mathbb{P}} \mid = \mid \mathbb{P} \mid\)
2.7. Reemplazar \(\mathbb{P}\) con \(\hat{\mathbb{P}}\)
2.8. Repetir búsqueda hasta que se cumpla el criterio de fin de búsqueda.
Representación de la solución
Una de las principales características de este algoritmo es la manera en la que se representa la solución a un problema. En la versión original del algoritmo, se propone, que se represente la solución como una cadena de bits, sin embargo, realmente puede ser una cadena de cualquier tipo de dato (números enteros, números reales, letras). Esta cadena siempre debe de ser del mismo tamaño en todas las soluciones del conjunto y cada posición define una característica o un comportamiento. Por ejemplo:
Individuo \(x_a\):

Individuo \(x_b\):

Función objetivo
Esta función es la que va a guiar el algoritmo hacia encontrar mejores soluciones. Normalmente el objetivo de un algoritmo genético es maximizar o minimizar el valor obtenido por una función:
\[G(x) = \max f(x)\]o
\[G(x) = \min f(x)\]A esa función \(f(x)\) se le conoce como función de aptitud. Si quisieramos crear un algoritmo genético para encontrar la representación binaria del numero 15 en 4 bits, una función de aptitud podría ser:
\[f(x) = \sum_{i=0}^{4} x_i \cdot 2^i\]Por lo tanto si tenemos dos individuos:
A: [0][1][0][1]
B: [1][0][0][1]
La aptitud del individuo A \(f(x_A)\) es 10 y del individuo B \(f(x_B)\) es 9, como estamos tratando de maximizar \(f(x)\), A es mejor solución que B.
Este ejemplo no es una aplicación práctica ni tampoco real de un algoritmo genético, encontrar una representación binaria es un problema de una sola solución, donde podemos llegar a la solución con exactitud, no es necesario aproximar el valor a través de búsqueda y optimización. Los algoritmos genéticos nos van servir para problemas a los cuales normalmente fallamos en encontrar una solución exacta y el espacio de búsqueda es más grande de lo que podemos abarcar.
Selección
Existen muchas formas para seleccionar los dos individuos que vamos a cruzar (paso 2.1). Los más populares son:
- Selección por ruleta
- Selección por torneo
- Selección por rango
Ruleta
En este método de selección, la probabilidad de un individuo de ser seleccionado es proporcional a su aptitud respecto a la población actual. Por lo tanto una solución \(x\) con aptitud \(f_x\), tiene una probabilidad de ser seleccionada
\[p_x = \frac{f_x}{\sum_{i=1}^{n}f_i}\]donde \(n\) es el tamaño de la población.
Si tenemos una población conformada por 4 soluciones \([x_1, x_2, x_3, x_4]\) con aptitudes \(f_{1} = 3, f_{2} = 4, f_{3} = 8, f_{4} = 1\) entonces las probabilidades de cada solución de ser seleccionada serán:
\[p_{1} = \frac{3}{3+4+8+1} = 0.19\] \[p_{2} = \frac{4}{3+4+8+1} = 0.25\] \[p_{3} = \frac{8}{3+4+8+1} = 0.5\] \[p_{4} = \frac{1}{3+4+8+1} = 0.06\]Rango
Es parecido a la selección por ruleta, pero la probabilidad de un individuo de ser seleccionado es de acuerdo a su posición en la población cuando es ordenada por aptitud. Si una solución \(x\) tiene posición \(r_x\) en la población de tamaño \(n\), la probabilidad de ser seleccionada es de:
\[p_x = \frac{n - r_x + 1}{\sum_{i=0}^{n}r_i}\]Por lo tanto, usando el ejemplo de la selección por ruleta, las probabilidades calculadas usando rangos serían:
\[p_{1} = \frac{4 - 3 + 1}{1 + 2 + 3 + 4} = 0.2\] \[p_{2} = \frac{4 - 2 + 1}{1 + 2 + 3 + 4} = 0.3\] \[p_{3} = \frac{4 - 1 + 1}{1 + 2 + 3 + 4} = 0.4\] \[p_{4} = \frac{4 - 4 + 1}{1 + 2 + 3 + 4} = 0.1\]Torneo
El método de selección por torneo es un poco más complicado que los otros dos. Consiste en escoger \(k\) individuos de la población y de esos \(k\) individuos, seleccionar al más apto. Al reducir el tamaño del torneo (\(k\)) podemos darle más posibilidad a individuos menos aptos. En el torneo se pueden manipular las probabilidades con las que un individuo gana el torneo. Esas probabilidades se pueden calcular con la ruleta o la selección por rango. Normalmente todos los individuos tienen la misma probabilidad de entrar al torneo y el individuo más apto es el que gana el torneo.
- Seleccionar \(k\) individuos de la población.
- Seleccionar al mejor individuo del torneo usando una probabilidad.
- Seleccionar al segundo mejor individuo del torneo usando una probabilidad.
.
.
.
Recombinación
Una vez seleccionados dos individuos de la población estos dos los combinamos para crear dos nuevas soluciones. La idea es que si la primera y la segunda solución son de buena calidad, los resultados de la recombinación deben de ser de buena calidad. Existen muchos métodos para combinar soluciones, el método que seleccionemos depende principalmente de la estructura de las soluciones. Hay problemas donde es necesario que ningún elemento de las soluciones este repetido, o soluciones donde no se pueden realizar operaciones aritméticas los elementos. La recombinación de un solo punto y la recombinación de k puntos, funcionan para soluciones binarias y también númericas.
La recombinación de orden 1 sirve para problemas donde las soluciones siempre contienen exactamente los mismos elementos y simplemente se altera el orden de los elementos.
Existen muchos más operadores de recombinación, estos son solo algunos muy usados.
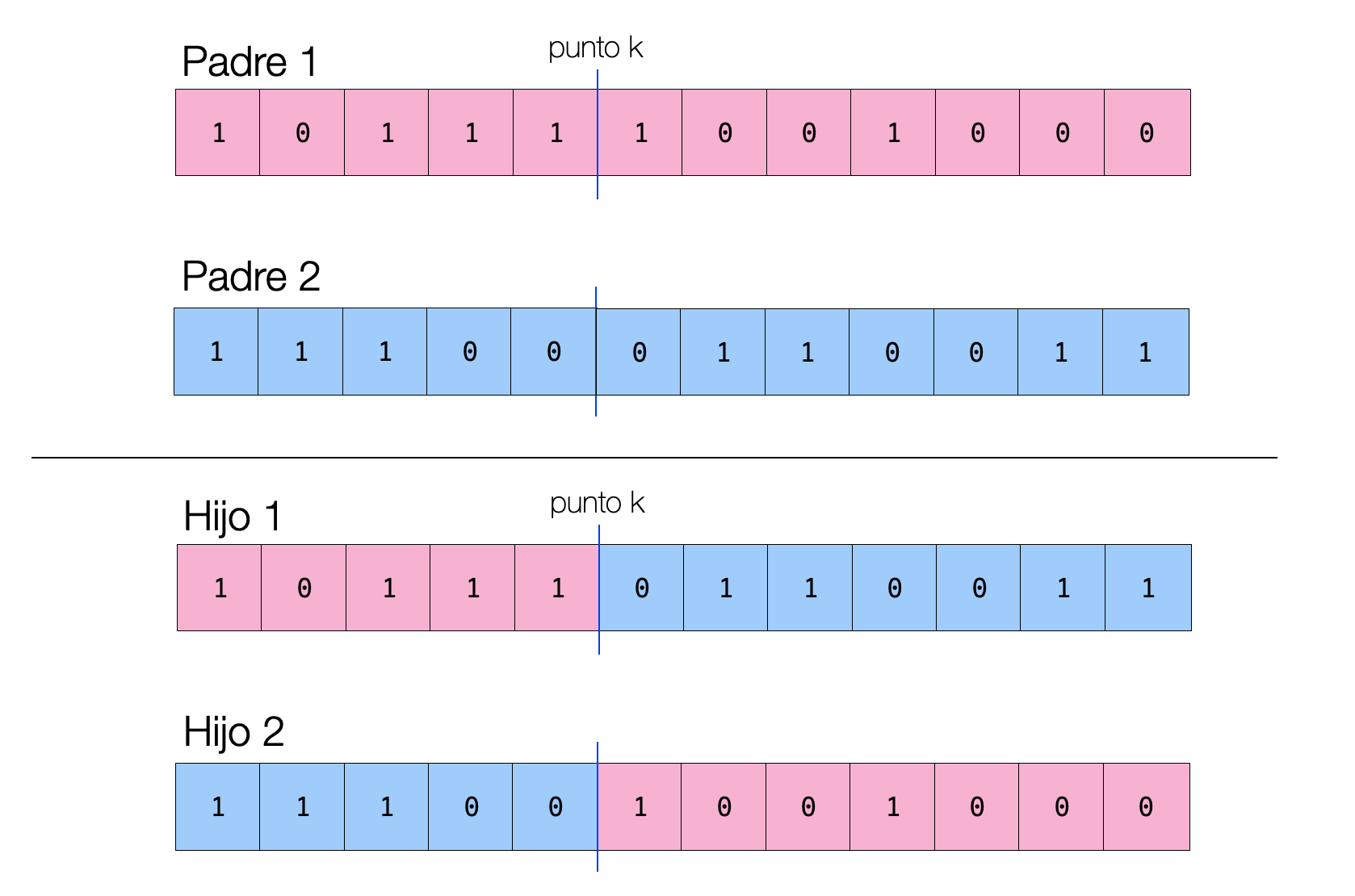
Recombinación de un solo punto
Si tenemos dos soluciones A y B, de tamaño \(N\):
- Se selecciona un número aleatorio \(k \mid 0 < k < N\)
- Los elementos del 0 al \(k\) del padre A se copian al hijo A.
- Los elementos del \(k\) al \(N\) del padre B se copian al hijo A.
- Los elementos del 0 al \(k\) del padre B se copian al hijo B.
- Los elementos del \(k\) al \(N\) del padre A se copian al hijo B.
Recombinación de k puntos
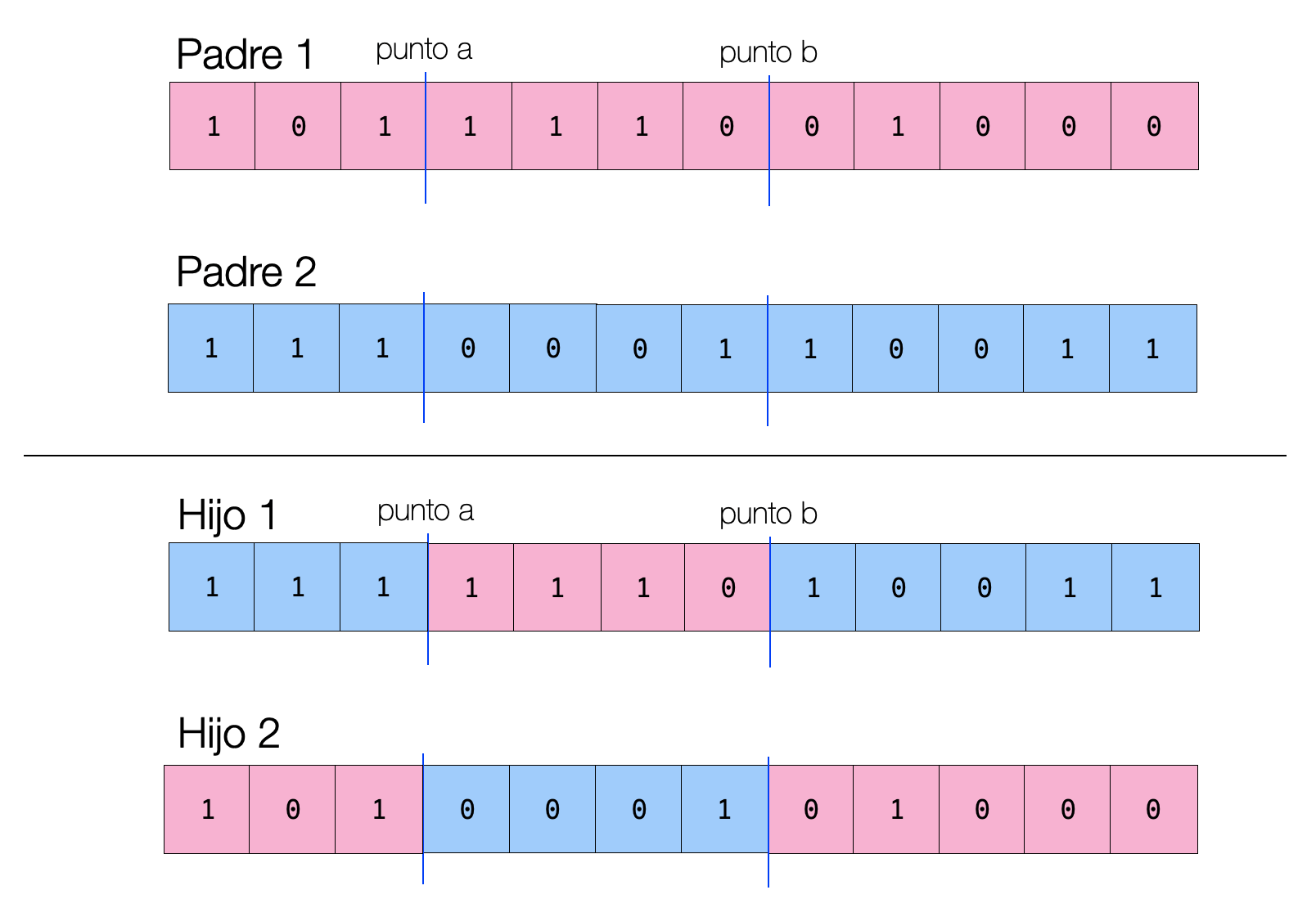
Es una generalización de la recombinación de un solo punto, pero seleccionando cualquier número de puntos. Cada solución padre es dividida por esos puntos en segmentos. Los segmentos se copian alternadamente a cada uno de los hijos:
Padre A:
Segmento 0 -> Hijo 1
Segmento 1 -> Hijo 2
Segmento 2 -> Hijo 1
.
.
.
Padre B:
Segmento 0 -> Hijo 2
Segmento 1 -> Hijo 1
Segmento 2 -> Hijo 2
.
.
.
Recombinación orden 1
La recombinación de orden 1 funciona solamente en problemas donde se requiere optimizar el orden de una serie de elementos. Un ejemplo clásico es el problema del viajero, donde dado un conjunto de ubicaciones, un viajero debe visitar solamente una vez cada ubicación de ese conjunto y volver a la ubicación inicial, minimizando la distancia total del viaje. En este problema las soluciones son representadas como un conjunto de números o identificadores únicos, donde cada uno de ellos representa una de las ubicaciones a las que el viajero debe de ir. El orden de esos valores, representa el orden en el que el viajero las visitará.
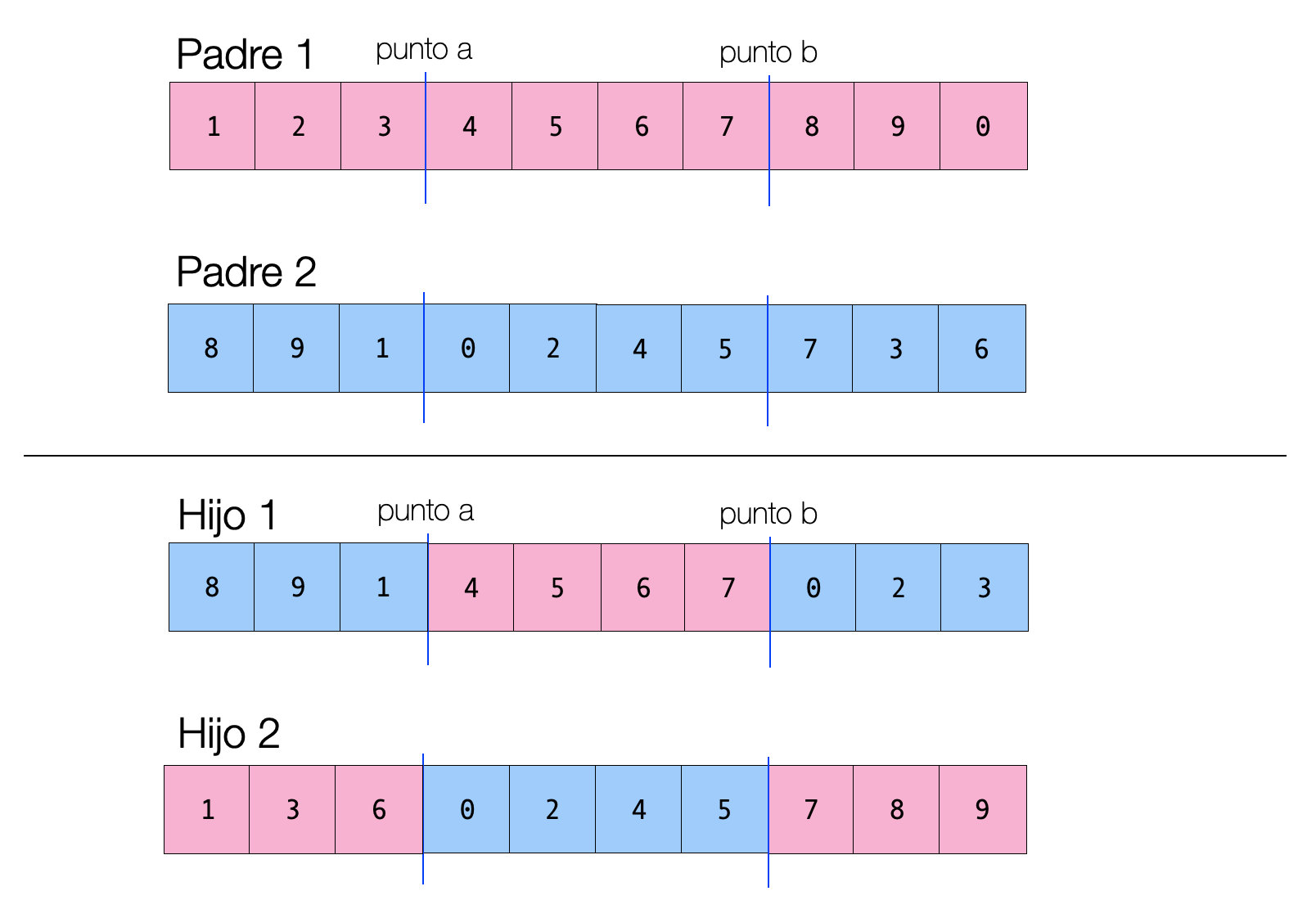
La recombinación de orden 1 funciona de la siguiente forma:
- Se selecciona aleatoriamente un conjunto de elementos consecutivos en el Padre 1 y se copian al hijo 1.
- Para cada elemento en el Padre 2 que no esta en el hijo 1, se copia al primer espacio vacío en el hijo 1.
- Se repite el procedimiento para el hijo 2.
Mutación
Las mutaciones son operadores que se aplican sobre una solución, para producir una solución similar pero con pequeñas alteraciones. Sirven para mantener diversidad dentro de la población y provocar soluciones más aptas. Al igual que las recombinaciones, hay muchos tipos de mutaciones y dependen del tipo de solución que tengamos. Algunas mutaciones son:
Intercambio
Se seleccionan dos elementos aleatoriamente de una solución y se intercambian.
Mutación de un solo punto
Se selecciona un elemento aleatoriamente en la solución y se cambia su valor por un número generado aleatoriamente.
Bit flip
En una solución binaria, se selecciona un elemento aleatoriamente en la solución y se cambia su valor (de 0 a 1, de 1 a 0).
Variantes
Elitismo
Se dice que un algoritmo genético es elitista cuando al reemplazar la población entre una generación y otra (paso 2.7), conservas la solución o las soluciones más aptas. De esta forma es imposible que se pierda calidad entre una generación y otra.
Creación de una población inicial
Definir el punto de partida de un algoritmo genético no es tan sencillo, para que funcione el algoritmo, es necesario que la población de soluciones al menos cumpla con estas dos características:
- Admisible: necesitamos generar soluciones que sean adecuadas al problema.
- Variada: entre más variedad de soluciones tengamos, el espacio de búsqueda es más amplio.
La forma más simple es creando arreglos aleatoriamente con la estructura de solución que definimos y después verificando que cumplan con las características que buscamos.